Case Volume and Loading for Long Range Precision: Part 1 The Basics

All long range competitive shooters agree that ammunition must be accurate at short range in order to be accurate at long range. They also know that this is a necessary condition, but not a sufficient one. In addition, the ammunition should have very low variation in muzzle velocity and the bullets should have a good ballistic coefficient.

Many factors influence muzzle velocity, and variation in these factors will lead commensurate variation in muzzle velocity. These include:

• Powder charge
• Case neck tension
• Case mouth uniformity
• Flash hole uniformity
• Primer consistency
• Bullet weight
• Bullet seating depth
• Case volume
• Recoil technique (strange but true – a topic for another post)

Each of these factors has a limit to which we can minimize variation, and at some point the effort to decrease variation leads to diminishing returns. In this article I will consider ammunition that is between reasonably and superbly controlled for most of the factors in the list and both how and how much controlling additionally for case volume can result in improved variation in muzzle velocity.

Suppose Case Volume was the Only Factor

The simplest place to start is with ammunition that is perfect in every way except for variation in case volume. Quickload and experiment have both shown that for many typical cartridges, powders, bullets, etc., muzzle velocity varies with case volume at a rate of approximately 20 fps to 30 fps per grain of H2O as a measure of case capacity. From here I will use “grains” in place of “grains H2O”, the “H2O” being implied.

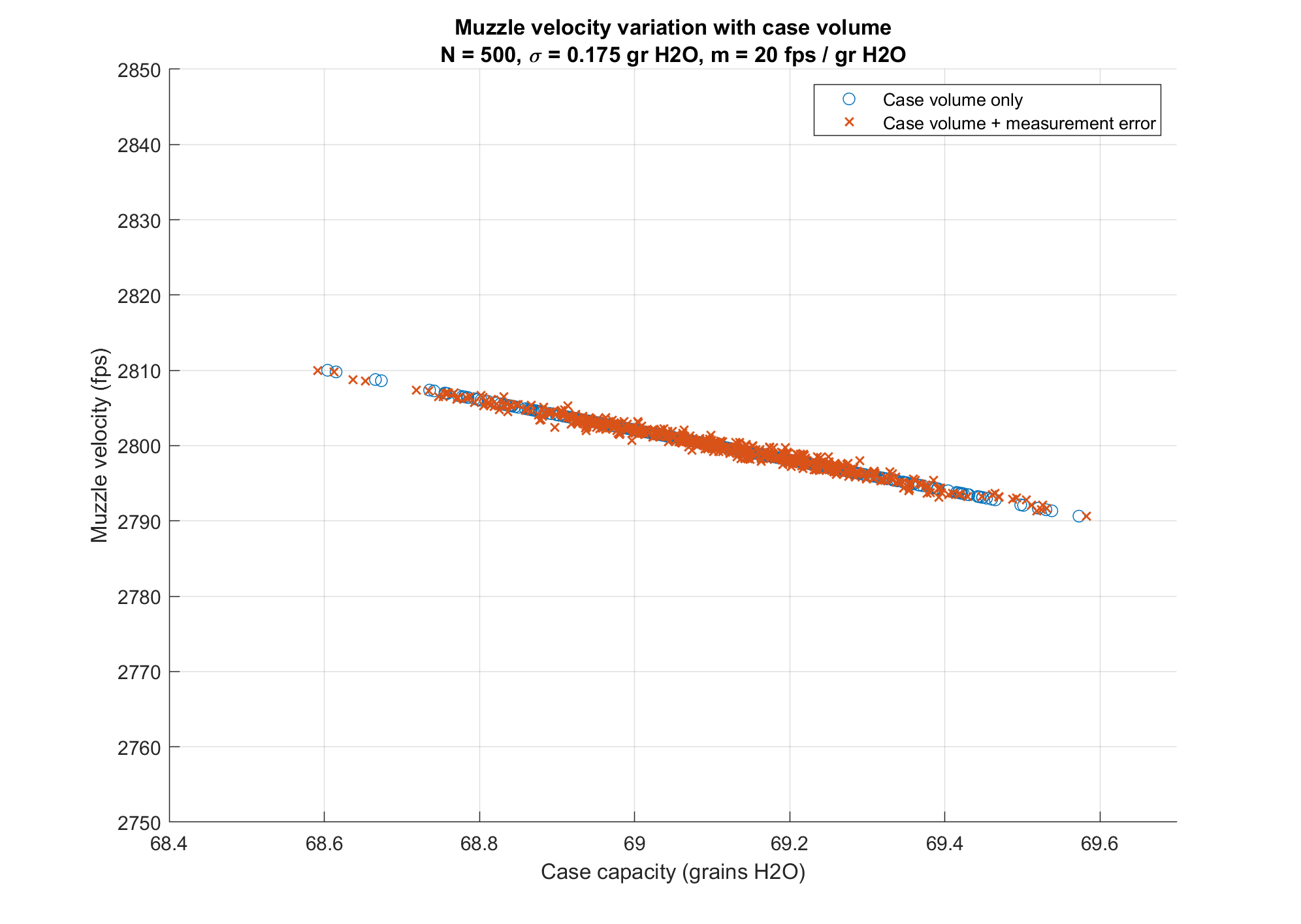
Consider ammunition from a simulated population of 500 284 Win cases in which the volume of the cases is normally distributed about a mean of 69.1 grains with a standard deviation of 0.175 grains. I got the mean and SD used here from real world measurement of 100 cases. Assuming that a case with 69.1 grains capacity produces 2800 fps muzzle velocity for a 180 grain Berger Hybrid, and a 20 fps per grain volume variation, a randomly generated population is shown in the following graph:

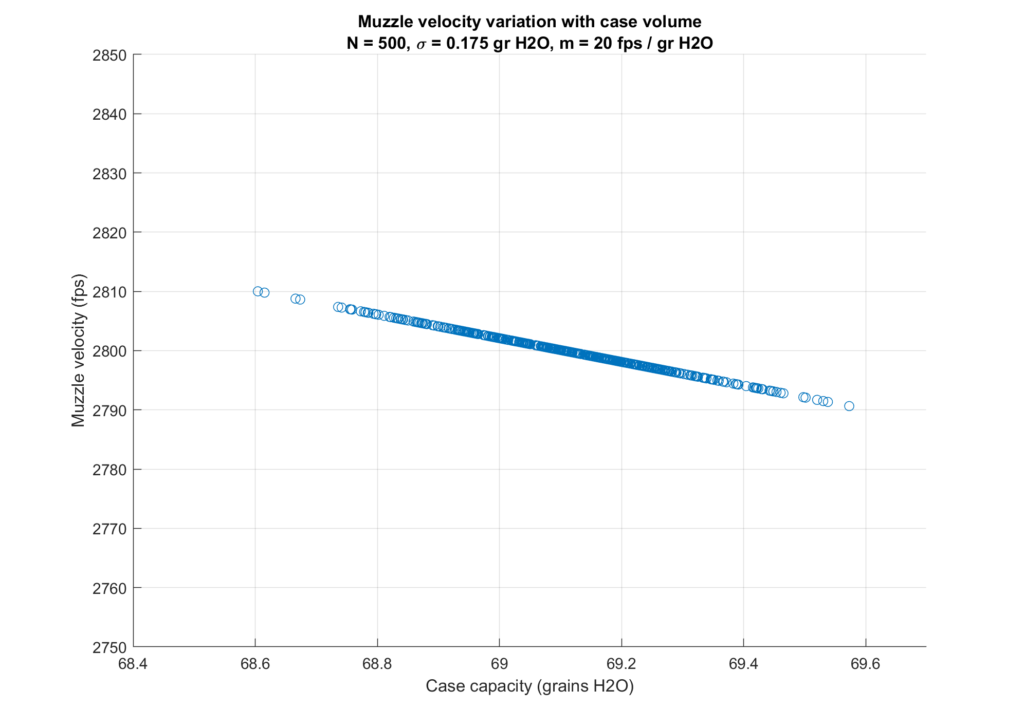
Most of the muzzle velocities are centered around 2800 fps as expected and we see a high an extreme spread of about 20 fps, which is not surprising since the population of cases has an extreme spread of case volumes that is about 1 grain.

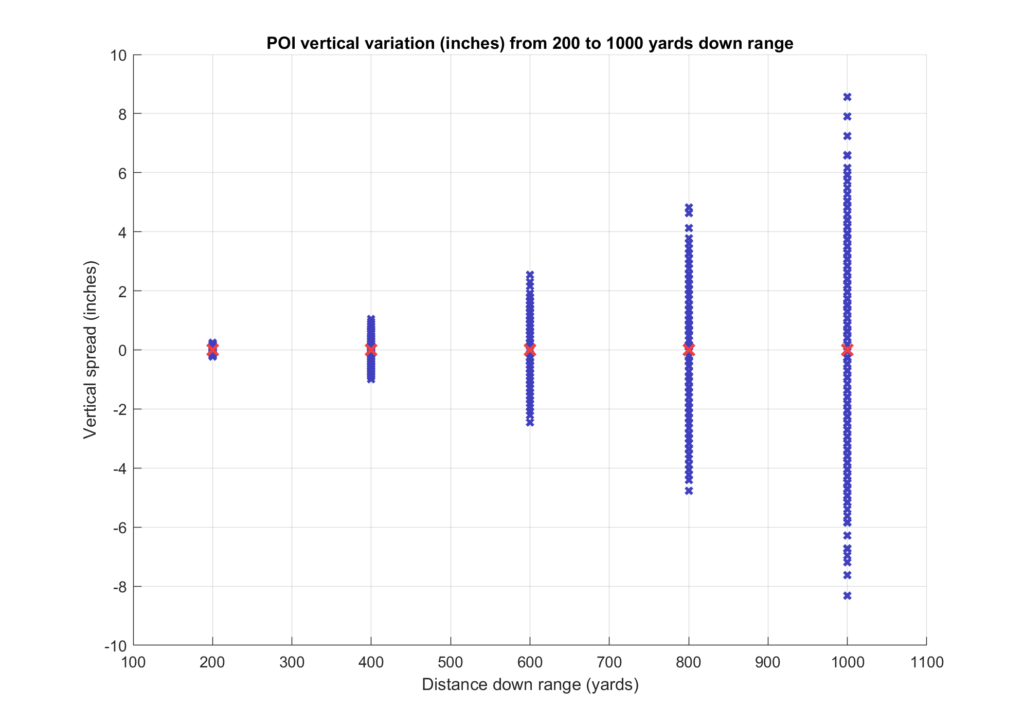
So what does this mean in practice? How will this otherwise perfect lot of ammunition shoot, all else being perfect? Using a typical G1 drag model for the Berger 180 Hybrid we get the following vertical distribution on paper from 600 to 1000 yards down range:

And again with vertical dispersion measured in minutes of angle instead of inches:

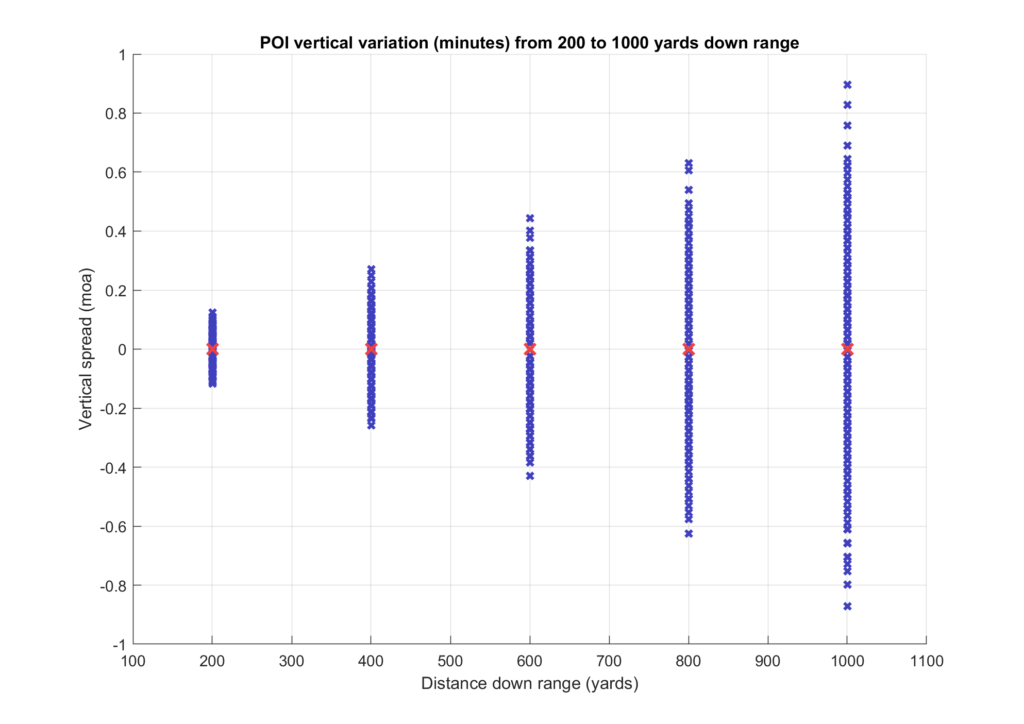
I prefer looking at the plot that shows POI vertical variation in minutes because it is easier to relate to score in high power rifle competition. At 200 yards the vertical variation is very small at just over +/- 0.1 minutes. I don’t know many people outside short range bench rest who would lose too much sleep over that. At 600 yards we’re approaching +/- 0.5 minutes, now that’s something. In Service rifle that can cost you an X or a point, and in F-Class we are definitely talking points to lose for a shot that would otherwise be near the inside edge of scoring a 10, and at 600 yards these days, X-count often separates winners and losers.

For those of us who shoot long range matches, which are typically from 800 to 1000 yards and shot on an LR or LR-F target, you can see that we’re talking serious points to lose with the vertical spread approaching +/- 1 moa.

Adding Measurement Error

We cannot measure case capacity perfectly. How much does measurement error influence our results so far? With the Bison Armory Case Capacity Gauge, I have performed some experiments to determine measurement error and a normal distribution with zero mean and standard deviation of 0.025 grains fits the data. Adding random measurement error to the muzzle velocity vs case capacity shown earlier, in which we keep the muzzle velocity where it was for the perfect case and only vary the measurement due to error we get the following:

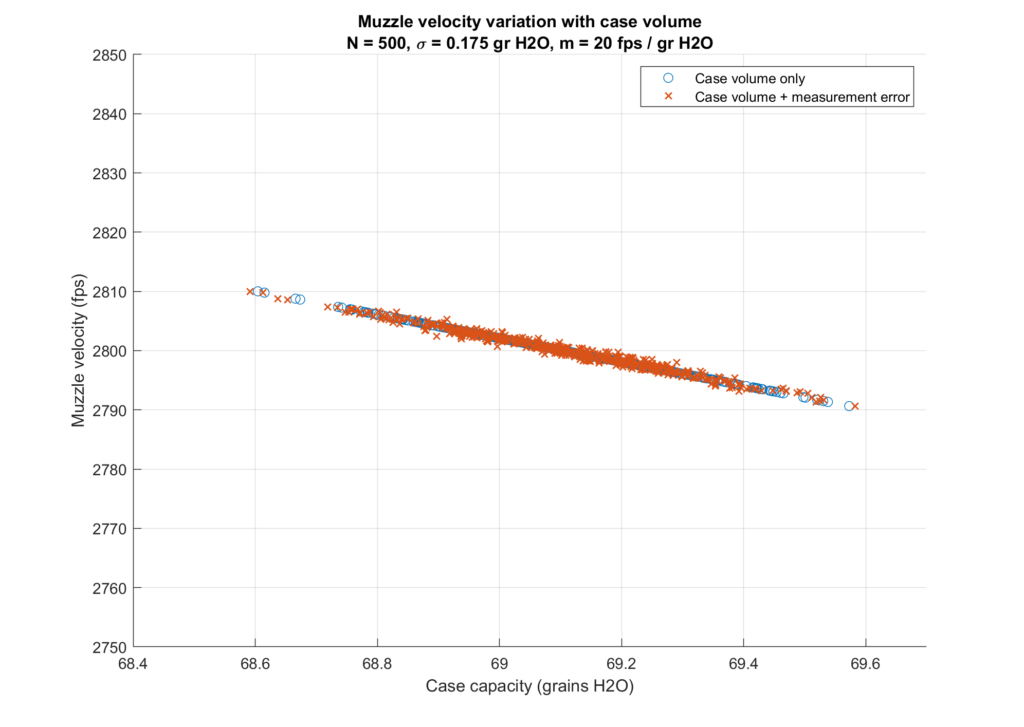
I think it is clear from this figure that case capacity measurement error is not a significant factor. If case volume was the only contributor to muzzle velocity variation, and we can measure case capacity as accurately as indicated in the figure, then it would be a simple thing to produce a batch of ammunition for a match that had minimal velocity spread.

Of course it’s not so simple. In the next post I’ll add muzzle velocity variation from all other sources and we’ll see how that complicates matters, and also how to make the best use of case capacity measurements to decrease muzzle velocity dispersion.